그래프(Graph)

 

그래프(Graph) 개요

그래프는 정점(Vertex)이라고 불리는 노드들의 집합과, 이 노드들을 연결하는 간선(Edge)들의 집합으로 이루어진 자료 구조입니다. 수학적으로 그래프 (G)는 정점들의 집합 (V)와 간선들의 집합 (E)의 순서쌍으로 정의됩니다. (G = (V, E))

그래프 종류

그래프는 간선의 특징에 따라 여러 종류로 나눌 수 있습니다.

 

• 무방향 그래프(Undirected Graph)
  • 간선에 방향이 없는 그래프
  • 간선((u,v))는 정점(u)와 정점(v)를 양방향으로 연결
• 방향 그래프(Directed Graph)
  • 간선에 방향이 있는 그래프
  • 간선((u,v))는 정점(u)에서 정점(v)로의 단방향 연결을 나타냄
• 가중치 그래프(Weighted Graph)
  • 각 간선에 가중치(비용, 거리 등)가 할당된 그래프
• 비가중치 그래프(Unweighted Graph)
  • 모든 간선의 가중치가 동일하거나 없는 것으로 간주하는 그래프
• 연결 그래프(Connected Graph)
  • 그래프의 모든 정점 쌍 사이에 경로가 존재하는 그래프
• 비연결 그래프(Disconnected Graph)
  • 연결되지 않은 하나 이상의 연결 요소로 이루어진 그래프
• 트리(Tree)
  • 사이클이 없는 연결 그래프
• DAG(Directed Acyclic Graph)
  • 사이클이 없는 방향 그래프

그래프의 표현 방식

그래프를 코드로 표현하는 일반적인 방법은 다음과 같습니다.

1. 인접 행렬(Adjacency Matrix)

인접 행렬은 (n x n) 크기의 2차원 배열을 사용하여 그래프를 표현합니다. 여기서 (n)은 그래프의 정점(노드)의 개수입니다. adj[i][j]는 정점 (i)에서 정점 (j)로 가는 간선의 존재 여부나 가중치를 나타냅니다.

무방향 그래프

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n = 5; // 정점의 개수
    
    vector<vector<int>> adj(n, vector<int>(n, 0)); // 0으로 초기화

    // 간선 추가 (무방향)
    adj[0][1] = 1;
    adj[1][0] = 1;

    adj[0][2] = 1;
    adj[2][0] = 1;

    adj[1][3] = 1;
    adj[3][1] = 1;

    adj[2][4] = 1;
    adj[4][2] = 1;

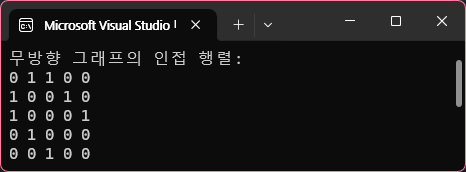
    cout << "무방향 그래프의 인접 행렬:" << endl;

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            cout << adj[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

 

가중치 무방향 그래프

#include <iostream>
#include <vector>

using namespace std;

const int INF = 1e9; // 연결되지 않은 경우 큰 값으로 표현

int main() {
    int n = 5; // 정점의 개수

    vector<vector<int>> adj(n, vector<int>(n, INF)); // INF로 초기화 (자기 자신은 0)
    for (int i = 0; i < n; ++i) {
        adj[i][i] = 0;
    }

    // 가중치 간선 추가 (무방향)
    adj[0][1] = 2;
    adj[1][0] = 2;

    adj[0][2] = 3;
    adj[2][0] = 3;

    adj[1][3] = 4;
    adj[3][1] = 4;

    adj[2][4] = 1;
    adj[4][2] = 1;

    cout << "가중치 무방향 그래프의 인접 행렬:" << endl;

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            if (adj[i][j] == INF) {
                cout << "INF ";
            }
            else {
                cout << adj[i][j] << " ";
            }
        }
        cout << endl;
    }

    return 0;
}

방향 그래프

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n = 5; // 정점의 개수

    vector<vector<int>> adj(n, vector<int>(n, 0)); // 0으로 초기화

    // 방향 간선 추가
    adj[0][1] = 1; // 0 -> 1
    adj[0][2] = 1; // 0 -> 2
    adj[1][3] = 1; // 1 -> 3
    adj[2][4] = 1; // 2 -> 4

    cout << "방향 그래프의 인접 행렬:" << endl;

    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            cout << adj[i][j] << " ";
        }
        cout << endl;
    }

    return 0;
}

2. 인접 리스트(Adjacency List)

인접 리스트는 각 정점에 연결된 인접한 정점들의 리스트를 사용하여 그래프를 표현합니다. adj[i]는 정점 (i)에 연결된 모든 정점들의 리스트(보통  std::vector)입니다. 가중치 그래프의 경우, 연결된 정점과 함께 가중치를 저장하기 위해 std::pair를 사용할 수 있습니다.

무방향 그래프

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n = 5; // 정점의 개수

    vector<vector<int>> adj(n);

    // 간선 추가 (무방향)
    adj[0].push_back(1);
    adj[1].push_back(0);

    adj[0].push_back(2);
    adj[2].push_back(0);

    adj[1].push_back(3);
    adj[3].push_back(1);

    adj[2].push_back(4);
    adj[4].push_back(2);

    cout << "무방향 그래프의 인접 리스트:" << endl;

    for (int i = 0; i < n; ++i) {
        cout << i << ": ";

        for (int neighbor : adj[i]) {
            cout << neighbor << " ";
        }
        cout << endl;
    }

    return 0;
}

가중치 무방향 그래프

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n = 5; // 정점의 개수

    vector<vector<pair<int, int>>> adj(n); // {연결된 정점, 가중치}

    // 가중치 간선 추가 (무방향)
    adj[0].push_back({ 1, 2 });
    adj[1].push_back({ 0, 2 });

    adj[0].push_back({ 2, 3 });
    adj[2].push_back({ 0, 3 });

    adj[1].push_back({ 3, 4 });
    adj[3].push_back({ 1, 4 });

    adj[2].push_back({ 4, 1 });
    adj[4].push_back({ 2, 1 });

    cout << "가중치 무방향 그래프의 인접 리스트:" << endl;

    for (int i = 0; i < n; ++i) {
        cout << i << ": ";

        for (const auto& edge : adj[i]) {
            cout << "(" << edge.first << ", " << edge.second << ") ";
        }

        cout << endl;
    }

    return 0;
}

방향 그래프

#include <iostream>
#include <vector>

using namespace std;

int main() {
    int n = 5; // 정점의 개수

    vector<vector<int>> adj(n);

    // 방향 간선 추가
    adj[0].push_back(1); // 0 -> 1
    adj[0].push_back(2); // 0 -> 2
    adj[1].push_back(3); // 1 -> 3
    adj[2].push_back(4); // 2 -> 4

    cout << "방향 그래프의 인접 리스트:" << endl;

    for (int i = 0; i < n; ++i) {
        cout << i << ": ";

        for (int neighbor : adj[i]) {
            cout << neighbor << " ";
        }

        cout << endl;
    }

    return 0;
}